Breaking Vectors Into Components
- University Short Cuts
- Jan 20
- 9 min read
Summary of Post
· Breaking vectors into components is tricky at first, but essential for solving physics and engineering problems.
· Common challenges include visualizing axes, switching to 3D, and relating vectors to axis.
· Use right triangles and trigonometry (“soh cah toa”) to find x, y, and z components.
· For 2D vectors, multiply the magnitude by the cosine or sine of the angle to get components.
· For 3D vectors, solve for the z component first, then use triangles to find x and y.
· Drawing diagrams and staying organized helps avoid mistakes.
Breaking vectors into components can be confusing at first. Personally, I struggled applying the math behind solving for components. I did find it convoluted at first, and I hope that’s why you are here to get things cleared up. Once you finally master solving for components of vectors, it will make many of the problems that build on this subject easier and more intuitive.
Many classes you could take use vectors. Normal math classes to physics, and engineering-based courses all are likely to use vectors. In physics, they are used in projectile motion problems and engineering courses to apply forces to objects. Then in math, for the pure mathematical concepts.
To start, why is it hard to find vector components in the first place? Well, one reason might be that you simply do not see the way the x and y axis is pointed in the problem. What causes you not to understand this part can be two-fold. One, you just don’t know where the x and y axis should be, or two, the problem is on an incline, which then messes with your thought process on where the x and y axis are. This confusion happens to me sometimes when I start with a problem, but I have learned how to recognize the components and stay calm. If you don’t stay calm, you can’t think as critically.
Another reason you don’t know how to break vectors into components is that you switched from a two-dimensional problem to a three-dimensional problem. This adds another part to the problem. This is where you must find not only the x and y components but the z component. If you do not know how to find the z component, that is understandable, and we can work on this just like you did with two dimensional problems.
The other reason you may not be able to solve components is that you do not see how the x and y axis relates to the vector. The vector itself is on the x and y axis. It is not floating in space like many problems make it look like it is. So, when the vector is at an angle, you can break it up into x and y coordinate directions. Another way to think about this is if the vector is pointed in a direction. There is a vector directly in the x direction with a magnitude…(value) plus a vector directly in the y direction with a magnitude…(value). The points of all three vector arrows will be pointed at the same point but from there respective directions.

Since we have covered the pain points of solving for components of vectors, let's move to a more conceptual way of thinking about components of vectors. The first and most obvious way of thinking about components is simply the x and y components, like we just talked about; however, this bleeds into thinking about the components as right triangles. As I stated before, if you have the vector and the x and y components pointed at one spot, as the photo above illustrates, and then you move either the x or y component over so that all the arrows make a triangle, you can now apply trigonometry to solve for values. Of course, you need values for the vectors and angles, but this will be given in the problem, and then you will have to solve for the other values.

Another way, other than trigonometry, to solve different components of a vector is using like triangles, which I will provide an example since you will run into it when you are solving components. You still will think of vectors the same way when solving, it is just simpler.
For the trigonometry I referenced earlier, you will need to know the unit circle, since this will help you solve the problems quicker. If you do not know the unit circle, I will link Nancy Pi’s Video here! This will help you understand the unit circle and memorize it. Also, you will need to be able to apply (soh cah toa), which are basic trigonometry functions that allow you to solve for angles and sides of right-angle triangles. I will link a helpful video here! A tip I use for trigonometry functions is that wherever the angle is, the side that is directly opposite of that is the o, and then I figure out the rest from there. It allows me to only have to remember one item. In my book Calculus One Made Simple, I will talk about some other trigonometric functions. If you want to learn more about trigonometry and calculus, buy my book on Amazon, linked here!
Now, the final way you will need to think about vectors conceptually is when the vectors are in three dimensions. This makes them harder to solve, but don’t throw out your triangle idea here, since you can think of it as several related triangles to get you your components. You will end up having a proxy triangle that doesn’t really mean anything, but it is there to help you solve the z-value. This proxy triangle sets you on the correct plan to solve your z value. I had trouble remembering to do this, and I started to remember it as a proxy set-up triangle. This is where I have f’ as one of the terms I solve for along with the z value. So hopefully, that is a little tip for you when you solve these problems. Additionally, it will make more sense when we get into three-dimensional problems. But we will stick to the normal two-dimensional problems first. This was simply to prime you and to get you to think about the process sooner, rather than thinking about it only when you see a three-dimensional problem. It's literally a plan of attack thought process.
Two-dimensional problem
We will start with a vector with a value of 10 at a 45-degree angle. Find the components in x and y. Now you can draw a picture, and I would recommend that you do this if you are just starting to learn how to solve these problems. The next step would be either to use your trigonometric functions to solve each component, or you could use the unit circle if you had it memorized. Luckily, I do, and that’s what we will do. So, we know that it is 45 degrees. Both x and y are root two over two, and it is positive because it is in the positive quadrant of the unit circle. Since we know this, we will then simply multiply ten by root two over two, and both x and y are this value, and the problem is done.

Now this makes sense because if you take the Pythagorean’s theorem and solve it for the vector, you will get ten. See below. Lastly, I should note that all these problems will be in the positive quadrant of the unit circle. If they where not some of the x or y values that we solved for could be negative.


This is the easiest problem you can have regarding vectors, so we will build up to harder problems to help you understand the details needed to solve each type of problem. What made this problem easy was the 45-degree angle. Since x and y are the same, it simplifies the math. With other problems, you will need to be able to understand which component will be the y and what will be the x. If you get this backwards, you will get the components wrong. Then, if you build on this topic, the whole problem will be incorrect because you got the components incorrect. Solving components is the base of the pyramid with these problems, and it needs to be mastered, which is why it is so important to take your time, even if you know how to solve the problems.
This next problem will be helpful to draw a free body diagram and split each component into parts that will make it easier to understand the problem. I know this requires more effort on your part. However, think of it this way: if you get the problem correct, you only must do it once, whereas if you get it wrong, you may have to do it again. So, it is best to stay organized while doing the problem.
In this case, we will have an angle that is not 45 degrees. So, you will need to think about which component will have more force and what trigonometric functions are needed to solve each component. I will provide a photo of the problem with the step-by-step solution below.

As you can see, it can be challenging to understand which side of the problem is. I suggest that you write out soh cah toa every time you come to a problem. This will help you see what side it what. It is so easy to get confused and mess up the components. So, take your time when solving.
We will use triangles to solve this next problem. That is what the problem gives us. It is just applying a ratio to get the components of the problem. Hopefully, this will come naturally to you, but if it doesn’t, I have fully worked out the problem for you. Keep in mind that the side you are solving for is the same side you will use on the little triangle to help solve for the component. For example, if you want a component and that little triangle has a 4 for the side that is similar to the y component, you will use that 4 in the numerator of the ratio, and the hypotenuse will be in the denominator. Then you will multiply by the total vector value. This will give you the component. Now that you have some understanding of the problem, I will give you an example.

Three-Dimensional Vectors
The final problem we will be going over is three-dimensional vectors. These are the hardest because of the additional component. You will need to be able to solve two triangles here to get the x, y, and z components. The additional set of complexity will trip people up. The other part of this is that the two triangles are not on a flat plane; they are perpendicular to each other. This is because of how the axes are oriented. On your paper, it will look like the triangles are flat, but don’t get tricked by this; you must relate this information to three dimensions, even though it is on two-dimensional paper.
In this problem, we will want to solve for the z value first since we are given a side and an angle rather than the x and y components. Once the z value is solved, you will want to solve the hypotenuse of the other triangle. This is the triangle that contains the x and y components. The reason you will have to solve the hypotenuse with the z component triangle is that there are too many unknowns in the x and y component triangle. This is what I referred to as the proxy triangle earlier in the text. Once the hypotenuse of the x and y component triangle is solved for, you can start solving the x and y components. In the problem, I call the hypotenuse of the x and y component triangle f’. This was simply for easy distinction. I suggest that you do this because it will allow you to have a standard when you are solving these problems and will allow you to have a lower likelihood of getting confused. I will now attach the problem below, see if you can solve the problem on your own.

At the end of this problem, I did a check this was to see if the magnitude of the total value of the vector matches the original value of the problem. Which it does, and the problem is correct. What I used to check the value is the Pythagorean theorem. This is for finding the hypotenuse of a triangle, which is what we broke apart when solving this problem.
In conclusion, I hope you have learned something today about vectors and can fully picture them in your mind. That part is important to know how to do it. If you still can’t, don’t worry, math will have plenty of other examples that will push you to understand this mental map. Also, if you enjoyed my work and want to get better at math, please consider buying my calculus one book called Calculus One Made Simple. I will link it here! Additionally, if you want to be more effective with your time, please consider buying my planner here! Finally, if you want to follow what I am doing, visit my YouTube channel, Alpine Digest.
Liability Disclaimer
The content provided on this blog is for informational purposes only and reflects the opinions of the author. While we strive for accuracy, we make no warranties or representations regarding the completeness or reliability of the information. Any actions you take based on the content of this blog are at your own risk. We are not liable for any errors or omissions, or for any consequences that may arise from the use of this information. Always consult with a qualified professional for advice specific to your situation.
© 2026 Universityshortcuts




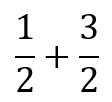


Comments