Simplifying Expressions
- University Short Cuts
- Nov 18, 2024
- 5 min read
Simplifying Expressions is essential to learning because it will be one of the things that can hold you back when you try to learn higher-level math. This is a fundamental concept and is one of the building blocks of your mathematical learning. You will Simplify Expressions all the time and it is used to get a simplified form of an equation. Much like a run-on sentence can be trimmed down an equation can be trimmed down as well. However, both sentences and equations have rules that one must follow to get to the desired expression.
Many additional basic concepts will be needed to do this like adding subtraction multiplying and dividing as well as finding a common dominator. If you cannot do any of these things by themselves it will be hard to see what you need to do when a complex expression is put in front of you. As you get better at Simplifying Expressions it will become very apparent to you and almost natural. However, at first, it can be very difficult and frustrating. So, I will lay out the basic skills you will need at the beginning of the article and then move to example problems. Much like a technique session and then a live game. To reinforce these skills.
Basic Skills
The basic skills that you need to know are shown below. I will start by adding exponents when two of the same variables are multiplied and taken to a power.
Expression One:

Adding exponents is simple but the trick is to remember this and then you may have to do it when finding a common denominator. Because of taking x to a fractional power as shown below.
Expression Two:

Keep in mind that the fractions can also be negative and that the power of ½ is simply the square root of the variable. However, I do not like this as much because it is simpler and more convenient in my option to see it in fractional form. See Expression Two for an example. Your teacher may want you to express the equation in root form so this is important to keep in mind.
Expression Two but is in root form:

Now another concept to keep in mind is that a negative exponent is simply a variable to a power that is in the denominator when positive. An example will explain this better. See Expression Three:
Expression Three:

We will move on to two full example problems to solve since this is the best way to learn math. Please keep these basic concepts in the back of your mind as you simplify the given expressions. So that you can start to build these pathways of problem-solving. Additionally, I suggest you follow along with the first two and then try to solve the rest on your own and only refer to this article to check your answer or if you get stuck.
Problem One:
Simplify the Exponential Expression that is given:

Step one: identify the like terms and the coefficients.
Blue and Red are like terms and green are coefficients.

Step two: Combine the like terms with one of the rules stated above. ( when like terms are multiplied the exponents are added).

Now moving to the next problem is a little different because we will add two more of the basic concepts covered above ( Common denominator and negative exponents ).
Problem Two:
Simplify the Exponential Expression that is given:

Step one: identify the like terms and the coefficients.
Blue, Red, and Purple are like terms and green are coefficients.
Coefficients are 1 for both the x and y terms so they will not be colored in the first step.

Step Two: bring both variables to the bottom.

Step Three: Find a common denominator.

As you can see this is a little more complicated even though the expression looks a lot simpler at the beginning. Again, it is important to remember your basics and it can be done easily with one step at a time.
Another important note is that you must know that anything to the power of zero is one. You may come across something that is very scary and is to a zero power. Just know this will save you a lot of headaches on homework and tests. See problem number three for an example.
Problem Three:
Simplify the Exponential Expression that is given:

Looks very scary but is just one….
Now for these next problems, I would like you to do them on your own. I also will not be color coding them because you will not have this luxury on a test or exam.
Problem Four:
Simplify the Exponential Expression that is given:

Step one: Break them out into multiplication and identify the like terms.

Step Two: add the exponents.

Problem Five:
Simplify the Exponential Expression that is given:

Step one: Break them out into multiplication and identify the like terms.

Step Two: Find a common denominator.

Step Three: Combine like terms.

Note: The expression could be simplified into roots if you would like.
Problem Six:
Simplify the Exponential Expression that is given:

Step one: Break them out into multiplication and identify the like terms.

Step Two: Combine like terms.

Problem Seven:
Simplify the Exponential Expression that is given:

Now I am not going to explain the steps. I will only give you the solution to the problem and not explain the steps. I want you to try these on your own that is the only way you will learn how to do these for an exam or test.

Problem Eight:
Simplify the Exponential Expression that is given:

Step One: Distribute the first term. This is another basic and important thing to know when simplifying expressions.

Hopefully, by now you are starting to get the hang of solving these types of problems. It does take a good amount of practice but I believe you can get quick at solving them. Try more textbook problems and check your answers with the back of the book. Remember that this is not going to go away and I would spend some time fully understanding how to simplify expressions. You may have to go through a couple of problems repeatedly to get the rhythm. I promise after some work it will come naturally to you. Additionally, I will be providing more topics in my blog on math and other subjects so please consider supporting me and adding your email to the email list to get up-to-the-minute updates on my blog.
Was this article helpful to your learning of Simplifying Expressions?
Yes
No
Liability Disclaimer
The content provided on this blog is for informational purposes only and reflects the opinions of the author. While we strive for accuracy, we make no warranties or representations regarding the completeness or reliability of the information. Any actions you take based on the content of this blog are at your own risk. We are not liable for any errors or omissions, or for any consequences that may arise from the use of this information. Always consult with a qualified professional for advice specific to your situation.
© 2024 Universityshortcuts





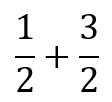

Comments