Least Common Denominator

University Short Cuts
Dec 2, 2024
5 min read

What is a Least Common Denominator or (LCD)? In mathematics, a Least Common Denominator is used so you can combine fractions by multiplying sets of fractions so all the Denominators are the same numbers. Finding the Least Common Denominator sounds and is simple but it can become complex if you don't have your multiplication table memorized or trying to find a denominator of multiple fractions.

To find the Least Common Denominator you will multiply the top and bottom of a given fraction by one. Since you can multiply anything by one it will be the same number you had before multiplying it by one. The fraction numbers will be large but it will be the same value. Cases where you need to find the least common denominator are where you are either adding or subtracting fractions. It doesn't matter if your fractions have numbers or variables this rule still applies. Each variance of the Least Common Denominator is better shown in examples than explained. So I will have a basic skill section followed by many examples.

Basic Skills

The basic skill you need for this is understanding what fractions are. Fractions are part of a whole number and can be displayed in decimals. Fractions can be scary given they are not as intuitive as decimal numbers. You can think of fractions as a pie that is cut up into many slices to equal one. If the numerator or the top of the fraction is bigger than the denominator then the fraction is greater than one and can be simplified to a mixed fraction which it was an improper fraction. So you will have a full pie and then some. The top of a fraction is called a numerator and this indicates how many parts of the given whole pie you have. Where the denominator indicates states how many parts there are in the whole. The image below will help you picture this better.

Another basic skill is multiplication and this is just taking a number times another number. So take two times three. This means you have two threes added together or three twos added together. Hopefully, you understand multiplication. I will not go further in depth. It should be noted that by multiplying fractions you do not need to find the Least Common Denominator. You just have to cross-multiply the two fractions to obtain the total.

Now moving to step-by-step example problems. The first one or two follow along then after that try to solve them on your own this will help cement the idea of the Least Common Denominator. Make sure you try the problems yourself at the end because this is the only way to start to understand this basic skill.

Problem One: Find the Simplyed expression for the following problem.

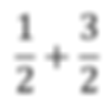
Step one: Since the bottom of the fraction is the same these terms can be added together and you do not have to do the Least Common Denominator. So combine like terms.

As you can see this first problem was very simple and was almost just as hard as adding two numbers together. Now we are going to move on to finding the Least Common Denominator for this next problem. So what you just did in the first problem will be the last step in the next problem.

Problem Two: Find the Simplyed expression for the following problem.

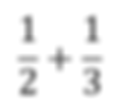
Step One: Since the Denominator has two different numbers you will have to find the Least Common Denominator to add the two fractions. To start you will have to think to yourself what number or two numbers will multiply together to get the smallest number that both products are the same. This is easier shown than said. We are going to multiply the 2 by a 3 and the 3 by a 2 not because they inverse but because the number 6 is the lowest value that both denominators can be to have the same denominators. Hence why it's called the Least Common Denominator.

Step Two: Now combine like terms. See the solution below.

Hopefully, this was not too complex for you and you understand the basic steps. We will now move on to the next problem which will be slightly harder. I recommend still following along with this problem.

Problem Three: Find the Simplyed expression for the following problem.

Step One: Now with this problem, it is the same as problem two but you have to essentially match three denominators. So you need to find a denominator that works for 12,4, and 3. Keep in mind you can only multiply by a value of one. Then you will finish by combining like terms again. See the solution below.

Now I would like you to start out by trying to solve the problems on your own so you can get some practice in and build this skill. Remember it is ok to struggle and it may take some time. But keep at it and you will understand it.

Problem Four: Find the Simplyed expression for the following problem.

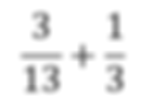
Step one: Find a Least Common Denominator. This problem is a little more annoying since 13 is a prime number so it will have to be used as your value for one as (13/13). Then the other side will have to be (3/3) because of this prime number problem. Lastly, combine like terms.

Problem Five: Find the Simplyed expression for the following problem.

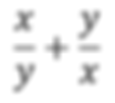
Step one: As you can see there are variables. Do not let this fluster you. You will still be applying the same basic steps. It's more apparent what your LCD has to be since multiplying by a number will not do anything. Yes the LCD is (XY or YX).

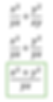
There is a good amount more of combining like terms in this example. That is ok if you didn't fully get this. Off the bat, it will take time and will depend on your mathematical experience or level you may not need to know this yet. But keep trying the examples on your own. Fortunately or unfortunately we will be moving to our last problem in this blog for LCD. This will be another step up and if you can do this you should be ready to rock on this topic.

Problem Six: Find the Simplyed expression for the following problem.

Step One: Try applying both basic steps of three and five to attack this problem. Then move on to combining like terms. Just watch out this problem will explode on you but stay calm and plug away it will simplify.

I hope these examples helped you understand LCD. It will be important to understand this topic because it will be used a lot moving forward in your math career. Remember to take your time. You may make simple mistakes and get frustrated if you try to rush the simplifying processes. I understand that this is easier said than done. Additionally, the more problems you do the more comfortable you will get with this topic. However, if you keep grinding through it. You may run into a block and if you keep pushing you will not get all that much out of your studying and learning. So I suggest taking a break for a short time to reset. I am going to have more topics posted on my blog that show examples for many classes so please consider following my website and keep up to date.

Liability Disclaimer

The content provided on this blog is for informational purposes only and reflects the opinions of the author. While we strive for accuracy, we make no warranties or representations regarding the completeness or reliability of the information. Any actions you take based on the content of this blog are at your own risk. We are not liable for any errors or omissions, or for any consequences that may arise from the use of this information. Always consult with a qualified professional for advice specific to your situation.