Solving Systems of Equations by Elimination and by Matrices
- University Short Cuts
- Oct 21, 2024
- 4 min read
This post I will be expanding upon an earlier post on Solving Systems of Equations by Substitution. These other two ways can make it easier to Solve Systems of Equations. However, there are some drawbacks. With the Elimination Method, it can be like factoring in the fact that you have to multiply both sides of some of the equations to get a variable or multiple variables to cancel out. This can be just as time-consuming as the Substitution Method. But a positive is if they are smaller equations they can be solved way faster than the Substitution Method. This may be good to understand for ACT application or during exams. If you're allowed to use a calculator you can make the calculator do the work by using Matrices. This is a must better option but may not be great if your teacher doesn't allow calculators. I will explain both methods below.
The Elimination Method For Systems of Equations
For this method, you organize the equations that are given by having your variables lined up. Then you ask yourself what number can I multiply one of the equations by to get rid of variables. However, this can be very difficult to do with three equations and three unknowns since you will have to multiply two equations by two different numbers to get two variables to cross out. Now that you have multiplied by the correct number you pretend like you are adding and subtracting like terms having the equations in a stacked format. Once done you will be left with one equation and one unknown which you can solve very easily.
The next step is to then solve for the other variables by plugging the variable you just found into one of the original equations. If it is a three unknown problems you may have to solve for some of the variables by substitution. If not it will be a pretty straightforward plug-and-chug problem. One thing to look out for is you may have to multiply by a negative so that a variable drops out. Also, watch your signs at the end when solving for a variable it's easy to get excited and then mess up the whole problem. Below I have attached two examples of the Elimination method.
Problem one:
Solving Systems of Equations By Elimination:
Find all the Variables in the Equation:
X + 3Y = 4
2Y +2X = 9

Be sure to check your answers by plugging in the numbers into both equations. Do this on exams if you have time so you know you have gotten the answers correct.
Problem Two:
Solving Systems of Equations By Elimination:
Find all the Variables in the Equation:
-X + 3Y = 4
2Y + 2X = 9

Again be sure to check your answers by plugging in the numbers into both equations. Do this on exams if you have time so you know you have gotten the answers correct.
Solving Systems of Equations By Matrices
This method is very nice and not very time-consuming you just organize your equations. Then you can use the matrix function of your calculator to solve for your missing variables. The example problem will give you a better understanding of how to solve it. But be sure to enter the numbers correctly into your calculator. then once both matrices are made. Make sure you take the matrix with the unknowns to the -1 power and then multiply it by the matrix with values on the other side of the equation. So it should be like this:
Matrix [B]: This is the matrix with the coefficients of the variables.
Matrix [A]: This is the matrix with the whole numbers on the other side of the equation.
2X + 3Y = 5
4X + 2Y = 7
You can plug in the values just like this because the equation is organized.
Now the formula for the matrix:
[B]*X = [A]
Where X is the variables and X is what we are solving for.
The Equation Solved for X:
X = [B]^(-1) * [A]
Solve the Problem from the calculator
X = 1.375
Y = 0.75
It will be displayed in this order on your calculator but in a matrix form.
Now I will give you another problem so you can try it again and this time it will be three equations with three unknowns.
Problem Three:
Solving Systems of Equations By Matrices:
Find all the Variables in the Equation:
X + 3Y -2Z = 3
-X + 4Y + Z =4
-X + Y -2Z = 9
Keep in mind the variables in the equations are organized already.

I hope this post helps your understanding of Systems of Equations and gets to the point. That is what has been a major problem with my learning. Lastly, if you want more content consider applying to the email list to get a reminder. I will be covering a lot of different topics and even example problems for math, science, and other subjects.
Liability Disclaimer
The content provided on this blog is for informational purposes only and reflects the opinions of the author. While we strive for accuracy, we make no warranties or representations regarding the completeness or reliability of the information. Any actions you take based on the content of this blog are at your own risk. We are not liable for any errors or omissions, or for any consequences that may arise from the use of this information. Always consult with a qualified professional for advice specific to your situation.
© 2024 Universityshortcuts



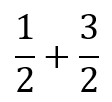


Comments