Solving Systems Of Equations By Substitution

Systems of Equations is an important topic to understand before going to college, especially in the STEM field. It is used in basic mathematics, Statics, Mechanics of Materials, and much more. In this post, I will provide some examples of problems with how to use the substitution method to solve these equations. Then at the end, I will give an application problem to Statics. You will be required to distribute and combine like terms in these types of problems. Which means they can get a little long for what you are solving for.

The first problem I have to solve is as follows:

X+3Y=4

2Y+2X=9

Find the value of all the variables in the two equations.

To solve this problem we are looking at where the two lines cross and this will give us our X and Y values. This is shown in the graph attached below. The red line is equation one and the blue line is equation two.

Now That you have an understanding of what we are looking for when solving the equations. We can go ahead and solve this problem.

Below is an attached photo of the solved problem laid out step by step.

Keep in mind when solving these problems to not make simple mistakes like combing the wrong terms or forgetting to change the sign of a value when it moves to the other side of the equal sign. PEMDAS must be used at all times and is another key basic skill that must be learned in order to follow the rules of mathematics.

Now moving on to a three-equation three-variable problem. We will be finding where three lines cross but in a three-denominational space instead of a two-denominational one. When using the substitution method it makes these problems more of a bear to solve and again make sure to check each like term and your signs.

Example Problem Two is as follows:

X+3Y-Z=8

3Y+4X+2Z=25

-2Z+3X-Y=3

Find the value of all the variables in the three equations.

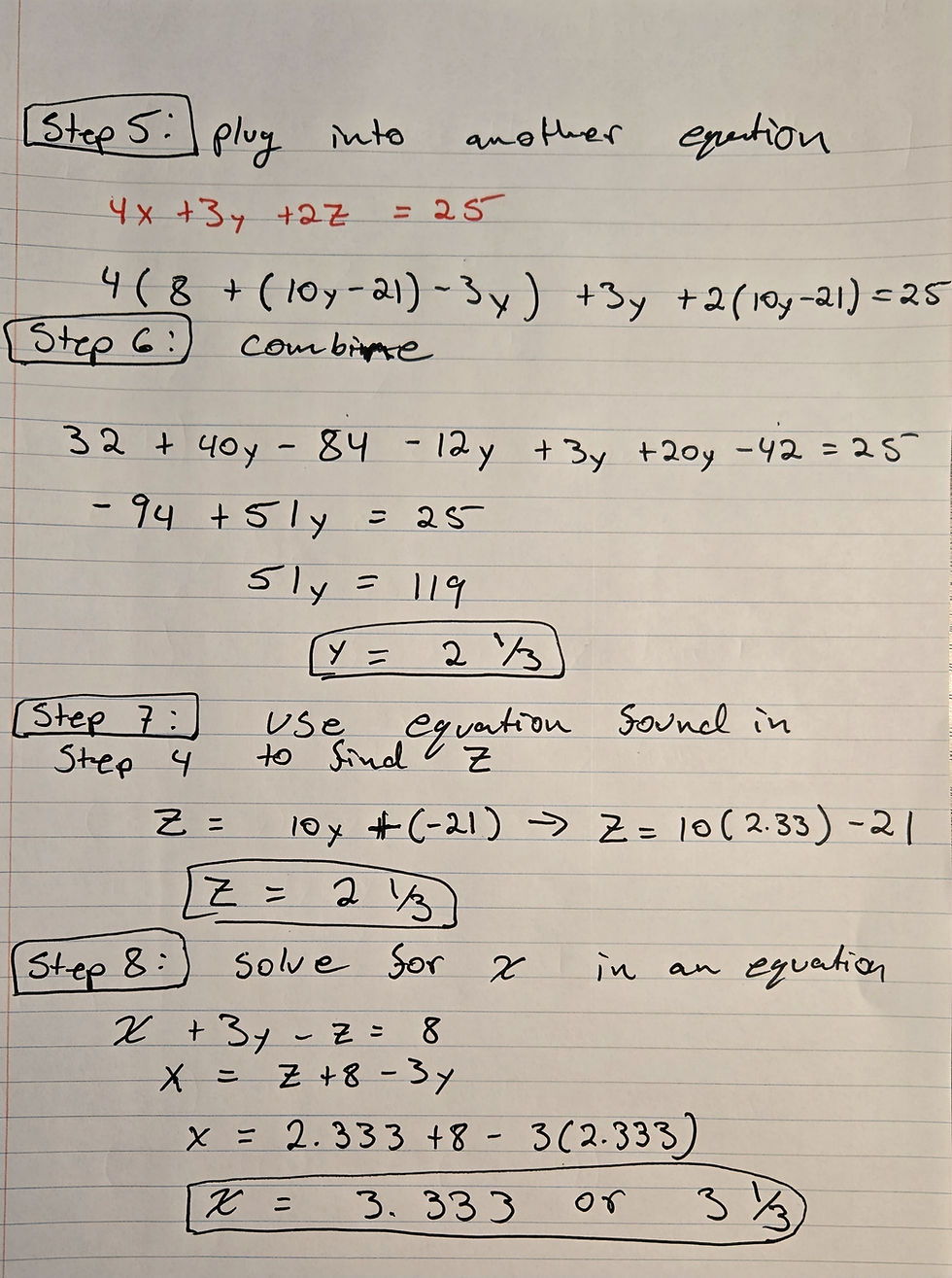
As you can see three equations make the problem much longer. It also is important to state that all three lines will intersect at X = 3.333, Y = 2.333, and Z = 2.33. Again these lines now are in three denominational spaces and no longer can only be plotted in two denominational spaces without multiple views. Since this can be a bear to solve like I said before you can use a matrixes function on your calculator to solve these equations much quicker and I will provide this information in later blogs.

My last problem is an applied problem of Systems of Equations in Statics so you can understand the importance of learning these basic concepts. But it has many other concepts I have not covered yet to solve these types of problems.

Example Problem Three:

As you can see there is a lot more math involved with solving this problem but it still comes back to the basic concept of Solving Systems of Equations. As always if you have any questions leave comments below and if you want additional content please sign up on the homepage and send over your email to be on the email list. Hopefully, this was helpful.

Liability Disclaimer

The content provided on this blog is for informational purposes only and reflects the opinions of the author. While we strive for accuracy, we make no warranties or representations regarding the completeness or reliability of the information. Any actions you take based on the content of this blog are at your own risk. We are not liable for any errors or omissions, or for any consequences that may arise from the use of this information. Always consult with a qualified professional for advice specific to your situation.

© 2024 Universityshortcuts